Analytical and Mathematical Modeling
Analytical modeling can provide a quick and cost effective way to gain an understanding of various fluid dynamic processes. Unlike the direct computational approach, where the full system of partial differential equations is simulated, an analytical approach generally involves the combination of simplified equations, integral momentum methods and empirical/semi-empirical correlations.
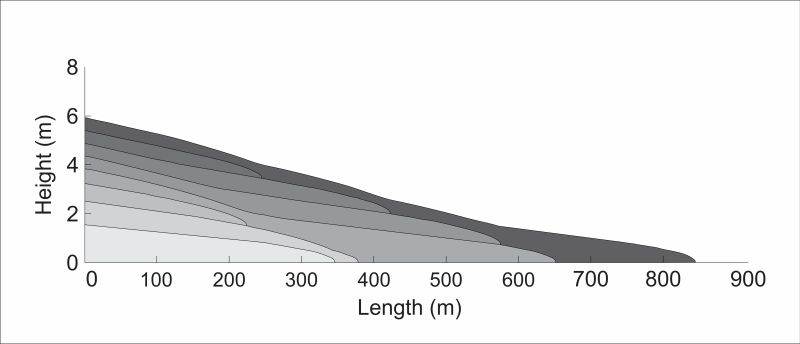
Modeling of non-Newtonian deposit profiles
Data Science and Statistical Analyses
To complement our laboratory services, experimental programs, and computational fluid dynamics abilities, Coanda offers a range of statistical and data analysis techniques to enhance the value of data for our clients.
Whether the data is provided by the client themselves or is from an experimental or numerical research program carried out by Coanda, we can analyze the data to look for latent structures and additional insights. This includes employing various regression methods, classification techniques, Monte-Carlo techniques, and predictive analyses.
Optimization of Processes and Process Geometries
Coanda can help clients optimize complex processes or geometries by combining a range of mathematical modeling tools and analysis services. Typically, the complexity of these systems mean there is a high-dimensional parameter space over which the optimization needs to be performed.
To overcome this challenge we use metamodeling. First, a model or metamodel is developed for each step of the process. These can come from different sources—response surface models, computational fluid dynamics models, empirical models—all of which Coanda can develop with the client and perform experiments for if necessary.
The (meta)models are then combined into a single coupled model where the outputs from one model act as inputs for another. Finally, taking in all the desired performance criteria and constraints, we use appropriate design space exploration and optimization algorithms to find optimal designs (or design changes) for the process.
Mathematical modeling allows for such global optimizations to be carried out on simple or complex design geometries alike. The resulting simplified system requires much less time to solve than direct numerical simulations of the full system. Also, performing “experiments” with analytical models are simple and low-cost, whereas physical experiments can have much higher costs and require considerably more time.

