CFD Fundamentals: Lagrangian / Eulerian Approach
Posted on April 22, 2021 Computational Fluid Dynamics
This post was originally published in two parts which have been combined below
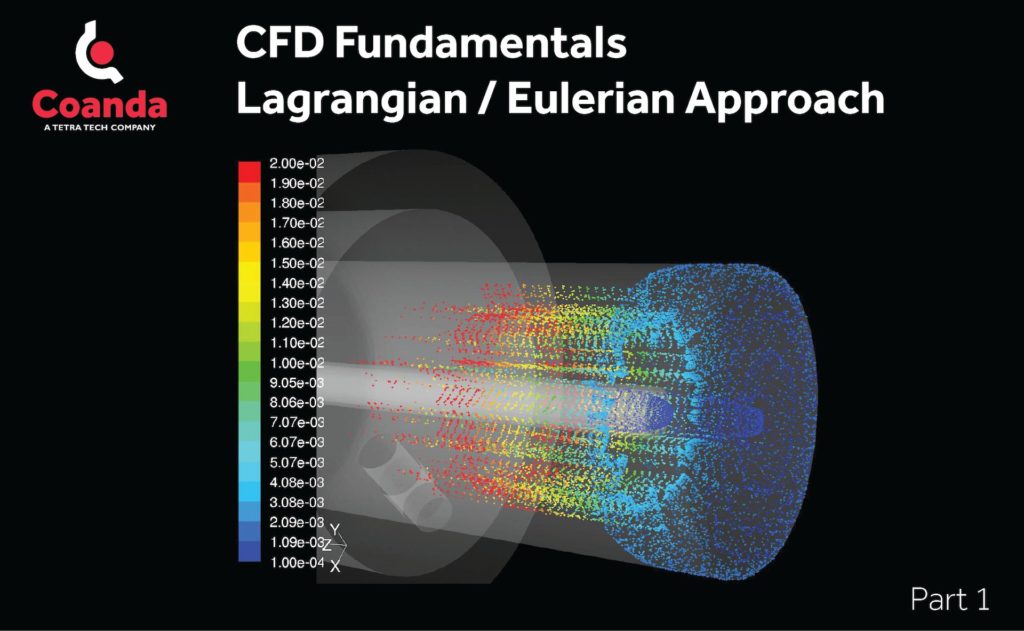
Part 1
A common challenge in CFD is to model the behaviour of a fluid (the continuous phase) carrying a dispersed phase comprising particles, droplets or bubbles. This situation arises in a variety of industrial applications, including slurry transport, catalytic cracking and gas scrubbers.
The two most popular approaches, Lagrangian and Eulerian, are distinguished by the reference frame in which the governing equations for the dispersed phase are formulated.
In the Lagrangian approach, the trajectory of a particle is determined via a force-momentum balance in the particle reference frame. For example, drag is calculated based on the relative velocity of the fluid surrounding a particle. Typically, it is cost-prohibitive to track every single particle in the dispersed phase, and instead, trajectories are calculated for a smaller, statistically-representative number of ‘super-particles’ with an equivalent mass flow rate. Varying degrees of coupling between the dispersed and continuous phases can be accounted for, and this approach can be particularly efficient where the effects of particles on the continuous phase are negligible.

Part 2
Our previous post covered the Lagrangian approach to one of the most common challenges in CFD; How to model the behaviour of a fluid (the continuous phase) carrying a dispersed phase comprising particles, droplets or bubbles.
In the Eulerian approach, equations describing the transport and exchange of mass, momentum and energy of the continuous and dispersed phases are formulated on a common (fixed or moving) reference frame. The concept of ‘volume fraction’, i.e. the proportion of each phase in a local (small) volume of the domain, is introduced, so that continuity can be maintained. Although the trajectories of individual particles are not computed, the phase volume fraction provides a very useful indication of the bulk behaviour of the dispersed phase, e.g. regions of accumulation. While this approach is considerably more expensive than Lagrangian modelling, it is particularly valuable where there is strong interphase-coupling and the dispersed phase occupies a high volume fraction.



